Назад

Олимпиадная задача: площадь треугольника PBQ и равенство площадей (Планиметрия, 8–10 класс)

Задача 211915 • Сложность: 3 • 8-10 класс
Задача
Угол B при вершине равнобедренного треугольника ABC равен 120°. Из вершины B выпустили внутрь треугольника два луча под углом 60° друг к другу, которые, отразившись от основания AC в точках P и Q, попали на боковые стороны в точки M и N (см. рис.). Докажите, что площадь треугольника PBQ равна сумме площадей треугольников AMP и CNQ.
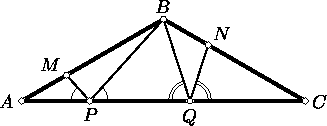
Решение

  Отразим картинку относительно основания AС (см. рис.). Заметим. что треугольники ABM1 и B1BN1 равны (один получается из другого поворотом на 60° вокруг точки B).

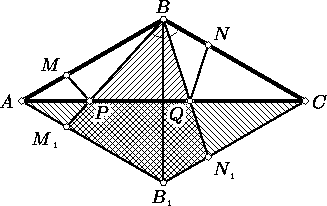
  Первый способ. Нам достаточно доказать, что  SBPQ = SAPM1 + SCQN1.

  Добавив к обеим частям SM1PQN1B1, сведём задачу к доказательству равенства  SACB1 = SBM1B1N1.  По доказанному

SBM1B1N1 = SM1BB1 + SB1BN1 = SM1BB1 + SABM1 = SABB1 = SACB1.   Второй способ. Из этого следует, что  MB = M1B1 = N1C.  Проведём отрезок MN1, пересекающий AC в точке O (см. рис.).

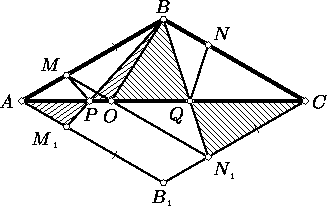
  В силу симметрии отрезок NM1 пройдёт через ту же точку O. Так как отрезки MB и N1C параллельны и равны, то MBCN1 – параллелограмм, а BON1C – трапеция. Значит,  SBOQ = SCN1Q = SCNQ  (см. задачу 154961). Аналогично  SBOP = SAM1P = SAMP.  Значит,

SPQB = SBOP + SBOQ = SAMP + SCNQ.

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет