Олимпиадная задача по планиметрии: угол BAC в треугольнике ABC, 8

Олимпиадная задача по планиметрии: прямая XY и угол BAC в треугольнике ABC

Задача

Вписанная окружность касается сторон AB и AC треугольника ABC в точках X и Y соответственно. Точка K– середина дуги AB описанной окружности треугольника ABC (не содержащей точки C). Оказалось, что прямая XY делит отрезок AK пополам. Чему может быть равен угол BAC?

Решение

Пусть отрезки XY и AI пересекаются в точке S. Как известно, KI = KA (см. задачу 153119), то есть высота KT треугольника AKI является его медианой. Так как XY ⊥ AI, то XY || KT, а поскольку XY делит сторону AK пополам, то XY– средняя линия треугольника AKT. Значит, AS : ST = 1 : 3; при этом XS – высота прямоугольного треугольника AXI, откуда ^AS/_ST = (^AX/_XI)², 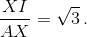Значит, ∠XAI = 60° и ∠BAC = 2∠XAI = 120°.