Назад

Олимпиадная задача по планиметрии: точка пересечения медиан и высот в треугольнике

Задача 211879 • Сложность: 3 • 9-10 класс
Задача

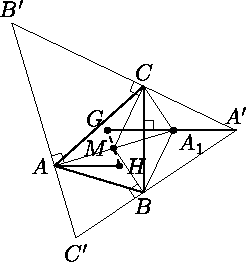
В неравнобедренном треугольнике ABC точки H и M – точки пересечения высот и медиан соответственно. Через вершины A, B и C проведены прямые, перпендикулярные прямым AM, BM, CM соответственно. Докажите, что точка пересечения медиан треугольника, образованного проведёнными прямыми, лежит на прямой MH.

Авторы:
Емельянов Л. А.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Всероссийская олимпиада по математике 2007-2008 Заключительный этап
Количество версий:
5
Решение
  ПустьA'B'C'– треугольник, образованный проведёнными прямыми (см. рис.) иG– точка пересечения его медиан. Мы докажем, чтоMявляется серединой отрезкаGH.   Достроим треугольникBMCдо параллелограммаBMCA1. ОтрезокMA1делит сторонуBCпополам, поэтомуA1лежит на прямойAM, причём AM = A1M.  Кроме того,  BA1||MC⊥A'B'  и  CA1||MB⊥A'C',  поэтомуBA1иCA1– высоты треугольникаBA'C. Значит,A1– ортоцентр этого треугольника и  A'A1⊥BC.   Стороны треугольникаBA1Mперпендикулярны сторонам треугольникаA'B'C'соответственно, поэтому эти треугольники подобны, причём соответствующие прямыеBCиAG, содержащие медианы этих треугольников, перпендикулярны. Значит, прямаяA'Gсовпадает с прямойA'A1. ПустьG'– точка, симметричная точкеHотносительноM. ТреугольникиAHMиA1G'Mсимметричны относительноM, поэтому  A1G' || AH⊥BC.  Отсюда следует, чтоG'лежит на прямойA'G. АналогичноG'лежит на прямойB'G, то естьG'совпадает сG.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет