Олимпиадная задача по планиметрии для 8-10 класса: пересечение прямоугольников
Задача
На плоскости нарисовано несколько прямоугольников со сторонами, параллельными осям координат. Известно, что каждые два прямоугольника можно пересечь вертикальной или горизонтальной прямой. Докажите, что можно провести одну горизонтальную и одну вертикальную прямую так, чтобы любой прямоугольник пересекался хотя бы с одной из этих двух прямых.
Решение
Лемма.Пусть в семействе прямоугольников любые два можно пересечь вертикальной прямой. Тогда их все можно пересечь вертикальной прямой.
Доказательство.Рассмотрим прямоугольник с самой левой правой границей и прямоугольник с самой правой левой границей. По условию их можно пересечь прямой. Тогда у любого из оставшихся прямоугольников левая граница будет левее этой прямой, а правая – правее, то есть прямая пересечет все прямоугольники. Лемма доказана.
Перейдем к решению задачи. Предположим противное. Назовем два прямоугольника разделенными, если их нельзя пересечь вертикальной прямой. Рассмотрим все пары разделенных прямоугольников. В каждой паре рассмотрим прямую, на которой лежит самая нижняя из их горизонтальных сторон; пусть h – самая высокая из этих прямых. Возможны два случая.
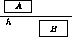
- Пусть не существует пары разделенных прямоугольников, лежащих ниже h . Проведем прямую h и рассмотрим все прямоугольники, не пересеченные ею. Если среди них нет пары разделенных, то по лемме их можно пересечь вертикальной прямой, и утверждение задачи доказано. Пусть такая пара прямоугольников(A,B)нашлась (см. рис.) . Тогда по предположению один из них (скажем, A ) лежит выше h . Из выбора h теперь следует, что нижняя сторона прямоугольника B лежит ниже h , а значит, и весь он лежит ниже h . Значит, эти прямоугольники нельзя пересечь ни вертикальной, ни горизонтальной прямой – противоречие.
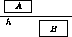
- Пусть существует пара(C,D)разделенных прямоугольников, лежащих ниже h . По выбору h , существуют также два разделенных прямоугольника A и B , лежащие не ниже h . Будем считать, что прямоугольник A лежит левее, чем B , а прямоугольник C – левее, чем D . Пусть для определенности правая сторона A находится не правее, чем правая сторона C (см. рис.) . Тогда прямоугольники A и D также разделены, при этом один из них лежит не ниже h , а другой – ниже h . Значит, эти два прямоугольника нельзя пересечь ни вертикальной, ни горизонтальной прямой. Противоречие.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь