Олимпиадная задача по планиметрии: параллельность прямых в треугольнике ABC, 8–10 класс
Задача
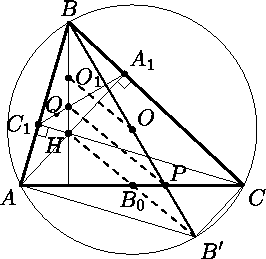
В неравнобедренном остроугольном треугольнике ABC проведены высоты AA1 и CC1, H – точка пересечения высот, O – центр описанной окружности, B0 – середина стороны AC. Прямая BO пересекает сторону AC в точке P, а прямые BH и A1C1 пересекаются в точке Q. Докажите, что прямые HB0 и PQ параллельны.
Решение
Пусть точка O1 – середина отрезка BH. Точки A1 и C1 лежат на окружности с диаметром BH, то есть с центром в точке O1.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет