Назад

Олимпиадная задача по планиметрии для 9–10 классов от Акопяна А. В.: Докажите равенство OM и ON

Задача 211871 • Сложность: 3 • 9-10 класс
Задача

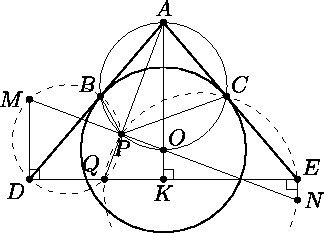
Окружность ω с центром O вписана в угол BAC и касается его сторон в точках B и C. Внутри угла BAC выбрана точка Q. На отрезке AQ нашлась такая точка P, что  AQ ⊥ OP.  Прямая OP пересекает описанные окружности ω1 и ω2 треугольников BPQ и CPQ, вторично в точках M и N. Докажите, что  OM = ON.

Авторы:
Акопян А. В.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Всероссийская олимпиада по математике 2007-2008 Заключительный этап
Количество версий:
5
Решение

  Пусть окружности ω1 и ω2 пересекают лучи AB и AC в точках D и E соответственно. По теореме о произведении отрезков секущих

AB·AD = AP·AQ = AC·AE.  Так как  AB = AC,  то  AD = AE.  Пусть K – середина DE. Тогда прямая AK является медианой, высотой и биссектрисой равнобедренного треугольника ADE, в частности, AK проходит через O.

  ТочкиA, B, C, P, Oлежат на окружности с диаметромAO. Из вписанных четырёхугольниковABPC, BPQD, CPQE: ∠PQD= 180° – ∠PBD= ∠ABP= 180° – ∠ACP= ∠PCE= 180° –PQE,  поэтому точкаQлежит на отрезкеDE. Так как четырёхугольникPQDMвписанный, то  ∠MDQ= ∠MPQ= 90°,  отсюда  MD⊥DE.  Аналогично  NE⊥DE.  Таким образом,  MD || OK || NE  и  DK = KE.  Следовательно, OM = ON.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет