Олимпиадная задача: Фокусник и площадь выпуклого 2008-угольника, планиметрия 9-11 класс

Обозначим A=A2008. Диагонали, выходящие из вершины A , делят его на 2006 треугольников AA₁A₂ , AA2006A2007. Пусть AM₁ , A M2006– медианы этих треугольников. Покажем, что если фокусник назовет все пары точек(A, M_k), k = 1,2,.., 2006, то он сможет угадать площадь многоугольника. Обозначим через S_k площадь, называемую для прямой A M_k , а через2T_k – площадь треугольника AA_kA_k+1. Так как медиана делит треугольник на две равновеликих части, то S_k=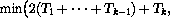 T_k+2(T_k+1+..+T2006)). При этом ясно, что S₁=T₁ , S2006=T2006. Заметим, что фокуснику достаточно вычислить значения всех T_k .

Пусть AL – прямая, делящая площадь многоугольника пополам. Заметим, что если отрезок AM_k по одну сторону от прямой AL , то фокуснику будут называть площадь многоугольника AA₁.. A_kM_k , а если по другую– то площадь оставшейся части. Поэтому до прямой AL значения S_k будут возрастать, а после– убывать. Таким образом, если S₁<..<S_n S_n+1>..>S2006(может оказаться, что n=1или n=2006), то при i=1,..,n-1мы имеем S_i=2(T₁+..+T_i-1)+T_i , откуда легко вычислить T_i ; аналогично они вычисляются при i=2006,..,n+1. Осталось вычислить T_n . Но S_n=2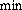(T₁+..+T_n-1,T_n+1+..+T2006)+T_n , откуда вычисляется T_n .

Ответ задачи отсутствует