Олимпиадная задача по стереометрии: вписать тетраэдр в шар (10-11 класс)
Задача
Каждую грань тетраэдра можно поместить в круг радиуса1. Докажите, что весь тетраэдр можно поместить в шар радиуса 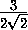 .
.
Решение
Заметим, что наименьший круг, содержащий нетупоугольный треугольник– это его описанный круг; для тупоугольного же треугольника это круг, построенный на его наибольшей стороне как на диаметре.
Пусть описанная сфера Ω нашего тетраэдра ABCD имеет центр O и радиус R . Предположим, что O лежит вне тетраэдра или на его границе. Рассмотрим ближайшую к O точку X тетраэдра. Возможны два случая:
-
X лежит внутри некоторой грани (скажем, ABC ). Тогда X является центром описанной окружности ω треугольника ABC , этот треугольник– остроугольный, поэтому радиус ω есть r
 1. При этом точки D и O лежат в разных полупространствах относительно ABC , и сфера c центром в X и радиусом r содержит сферическую шапочку сферы Ω , содержащую ABCD . Значит, эта сфера содержит и ABCD .
1. При этом точки D и O лежат в разных полупространствах относительно ABC , и сфера c центром в X и радиусом r содержит сферическую шапочку сферы Ω , содержащую ABCD . Значит, эта сфера содержит и ABCD . -
X лежит на ребре AB . Тогда проекция O1 точки O на плоскость ABC лежит вне граней; более того, X является ближайшей к O1 точкой треугольника ABC . Поэтому O1 и C лежат в разных полуплоскостях относительно прямой AB , угол ACB тупой, и точка C лежит в шаре, построенном на AB как на диаметре (радиус этого шара по условию не превосходит 1). Аналогично, D лежит в этом шаре, поэтому шар содержит весь тетраэдр.
В обоих случаях тетраэдр поместился в шар радиуса 1.
Нам осталось разобрать только случай, когда O лежит внутри тетраэдра. В этом случае сумма объемов пирамид ABCO , ABDO , ACDO и BCDO равна VABCD , поэтому один из них не превосходит VABCD/4; пусть это объем пирамиды ABCO . Пусть луч DO пересекает плоскость ABC в точке D1 ; тогда 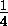

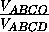 =
=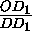 , поэтому OD1
, поэтому OD1
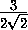 OD=
OD=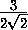 .
.
Рассмотрим ближайшую к O точку X на границе тетраэдра. Она не может лежать на ребре тетраэдра, потому что угол между одной из граней и отрезком OX будет острым. Значит, она лежит внутри одной из граней (скажем, ABC ), является центром ее описанной окружности, и по доказанному выше XO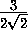
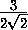 . Тогда радиус описанной окружности этой грани не менее
. Тогда радиус описанной окружности этой грани не менее 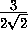 =
= 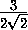 R . Так как по условию он не больше1, то R
R . Так как по условию он не больше1, то R
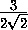 , и мы нашли шар требуемого радиуса, содержащий тетраэдр.
, и мы нашли шар требуемого радиуса, содержащий тетраэдр.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь