Олимпиадная задача по математике: Саша вырезает цифры из факториалов (9 класс, уровень 4)
Задача
Дима посчитал факториалы всех натуральных чисел от80 до 99, нашел числа,
обратные к ним, и напечатал получившиеся десятичные дроби на 20 бесконечных
ленточках (например, на последней ленточке было напечатано число 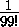 =0,
=0, 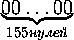 10715.. ).
Саша хочет вырезать из одной ленточки кусок, на котором записано N цифр подряд и нет запятой. При каком наибольшем N он сможет это сделать так, чтобы Дима не смог определить по этому куску, какую ленточку испортил Саша?
10715.. ).
Саша хочет вырезать из одной ленточки кусок, на котором записано N цифр подряд и нет запятой. При каком наибольшем N он сможет это сделать так, чтобы Дима не смог определить по этому куску, какую ленточку испортил Саша?
Решение
N=155.
Пусть на ленточках, на которых записаны числа1/k! и1/l! ( k<l ), нашлось по одинаковому куску из N подряд стоящих цифр.
Домножим числа1/k! и1/l! на степени 10 так, чтобы одинаковые куски
оказались сразу после десятичной запятой. Дробные части получившихся дробей10a/k! и10b/l! не могут совпадать. Действительно, в противном случае
число10a/k!-10b/l!=10a/((k+1)(k+2).. l)-10b/
l! целое; следовательно, числитель последней дроби делится на l .
Тогда на l делится и число10b . С другой стороны, ни одно число от 81 до 99 не является
делителем числа вида10b , так как каждое из этих чисел содержит в своем
разложении на множители хотя бы одно простое число, отличное от 2 и 5.
Рассматриваемые нами дробные части({10a/k!)} и({10b/l!)} могут быть записаны как обыкновенные
дроби со знаменателями k! и l! , а потому– и как дроби со
знаменателем99! , который делится на все числа80!, 81!, .., 99! ; следовательно,
их разность есть разность двух неравных дробей со знаменателем99! , и она не меньше1/99! .
С другой стороны, две правильные десятичные дроби, у которых
совпадают первые N цифр после запятой, отличаются меньше, чем на1/10N .
Таким образом,1/99!<1/10N . Из условия
следует, что 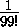 >
>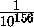 , поэтому N<156.
Таким образом, куска из 156 знаков всегда достаточно для того, чтобы
определить, из какой полоски он вырезан. С другой стороны, на полосках
с числами1/98! и1/99! есть одинаковые куски по 155
знаков:1/99!=0,
, поэтому N<156.
Таким образом, куска из 156 знаков всегда достаточно для того, чтобы
определить, из какой полоски он вырезан. С другой стороны, на полосках
с числами1/98! и1/99! есть одинаковые куски по 155
знаков:1/99!=0,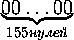 10715.. ,
а1/98!=99/99!=100/99!-199!=
0,
10715.. ,
а1/98!=99/99!=100/99!-199!=
0,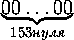 10715..-
0,
10715..-
0,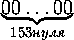 00107..=
0,
00107..=
0,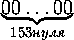 106.. ,
то есть на обеих полосках есть кусок
106.. ,
то есть на обеих полосках есть кусок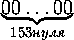 10.
10.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь