Назад

Олимпиадная задача по планиметрии для 8-10 классов с биссектрисой и окружностью

Задача 211845 • Сложность: 3 • 8-10 класс
Задача

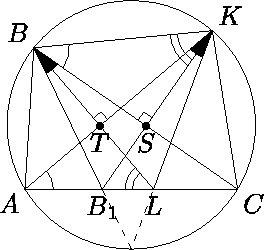
В треугольнике ABC проведена биссектриса BB1. Перпендикуляр, опущенный из точки B1 на BC, пересекает дугу BC описанной окружности треугольника ABC в точке K. Перпендикуляр опущенный из точки B на AK пересекает AC в точке L. Докажите что точки K, L и середина дуги AC (не содержащей точку B) лежат на одной прямой.

Авторы:
Астахов В.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Всероссийская олимпиада по математике 2006-2007 Заключительный этап
Количество версий:
4
Решение
ПустьSиT– основания перпендикуляров, опущенных изB1иBсоответственно наBCиAK(см. рис.).  ∠SBK= ∠LAT= α  как опирающиеся на одну дугуKC; поэтому  ∠B1LB= ∠ALT= 90° – α = ∠BKS= ∠BKB1,  то есть точкиB, B1,L, Kлежат на одной окружности. Отсюда  ∠BB1K=BLK= β,  и  ∠AKL= ∠TKL= 90° – β = ∠B1BS= ½ ∠ABC= ½ ∠AKC,  Это и означает, чтоKLпроходит через середину дугиAC.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет