Олимпиадная задача по планиметрии для 8–9 класса от Емельянова Л. А.
Задача
На стороне BC треугольника ABC выбрана произвольная точка D . В треугольники ABD и ACD вписаны окружности с центрами K и L соответственно. Докажите, что описанные окружности треугольников BKD и CLD вторично пересекаются на фиксированной окружности.
Решение
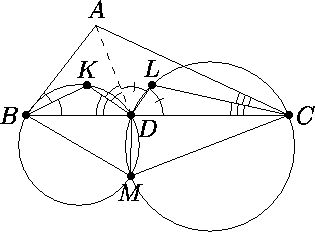
 BMC =
BMC =  BMD +
BMD +  CMD = (180o -
CMD = (180o -  BKD) + (180o -
BKD) + (180o -  CLD) =
CLD) =
 KBD +
KBD +  KDB +
KDB + LDC +
LDC +  LCD =
LCD =
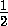 (
( ABD +
ABD +  ADB +
ADB +  ADC +
ADC +  ACD) =
ACD) =
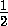 (
( ABD + 180o +
ABD + 180o +  ACD) =
90o+
ACD) =
90o+ 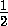 (
( ABD +
ABD +  ACD).
Величина угла BMC фиксирована, поэтому M лежит на фиксированной окружности
с хордой BC .
ACD).
Величина угла BMC фиксирована, поэтому M лежит на фиксированной окружности
с хордой BC .
Замечание. В решении используется, что точки A и M лежат по разные стороны от BC . Это нетрудно вывести из того, что углы BKD и CLD тупые.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет