Олимпиадная задача по планиметрии для 8-9 классов от Агахановa Н. Х.: площадь нового треугольника
Задача
У двух треугольников равны наибольшие стороны и равны наименьшие углы. Строится новый треугольник со сторонами, равными суммам соответствующих сторон данных треугольников (складываются наибольшие стороны двух треугольников, средние по длине стороны и наименьшие стороны). Докажите, что площадь нового треугольника не меньше удвоенной суммы площадей исходных.
Решение
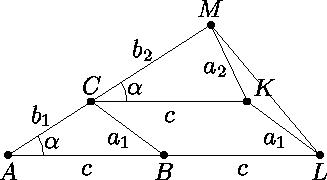
 b1
b1 c , a2
c , a2 b2
b2 c – длины сторон данных треугольников, α – их общий наименьший угол, α1 – наименьший угол в построенном треугольнике
со сторонами a1 + a2 , b1 + b2 , c + c . В этом треугольнике a1 + a2 – наименьшая сторона,
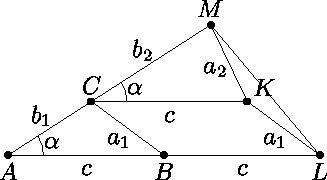
поэтому угол α1 лежит против нее и является острым. Рассмотрим треугольник AML с углом α при вершине A и боковыми сторонами AM = b1 + b2 , AL = c + c (рисунок).
Покажем, что α1
c – длины сторон данных треугольников, α – их общий наименьший угол, α1 – наименьший угол в построенном треугольнике
со сторонами a1 + a2 , b1 + b2 , c + c . В этом треугольнике a1 + a2 – наименьшая сторона,
поэтому угол α1 лежит против нее и является острым. Рассмотрим треугольник AML с углом α при вершине A и боковыми сторонами AM = b1 + b2 , AL = c + c (рисунок).
Покажем, что α1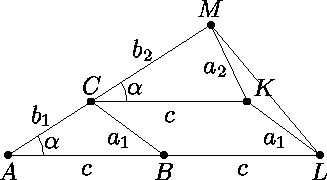 α ; для этого достаточно доказать, что ML
α ; для этого достаточно доказать, что ML a1+a2 .
Пусть B и C – точки на сторонах AL и AM соответственно такие, что AC = b1 , AB=c . Выберем точку K так, что BCKL –
параллелограмм. Тогда треугольники ABC и CKM соответственно равны исходным треугольикам,
поэтому из треугольника MKL получаем MK = a2 , KL = a1 , откуда по неравенству
треугольника ML
a1+a2 .
Пусть B и C – точки на сторонах AL и AM соответственно такие, что AC = b1 , AB=c . Выберем точку K так, что BCKL –
параллелограмм. Тогда треугольники ABC и CKM соответственно равны исходным треугольикам,
поэтому из треугольника MKL получаем MK = a2 , KL = a1 , откуда по неравенству
треугольника ML a1 + a2 , что и требовалось.
Отсюда S =
a1 + a2 , что и требовалось.
Отсюда S =  ( b1 + b2)(c + c) sin α1
( b1 + b2)(c + c) sin α1  (b1 + b2)c sin α
(b1 + b2)c sin α  2(
2( b1 c sin α +
b1 c sin α +  b2 c sin α) =
2(S1 + S2), что и требовалось доказать.
b2 c sin α) =
2(S1 + S2), что и требовалось доказать.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет