Олимпиадная задача по планиметрии для 9–11 классов: радиусы окружностей в треугольниках
Задача
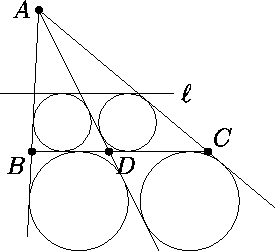
Точка D на стороне BC треугольника ABC такова, что радиусы вписанных окружностей треугольников ABD и ACD равны. Докажите, что радиусы окружностей, вневписанных в треугольники ABD и ACD , касающихся соответственно отрезков BD и CD , также равны.
Решение
Первое решение.
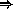
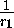 =
= 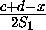 =
=
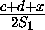 - 2
- 2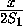 =
= 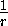 -
- 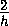 .
Аналогично можно получить, что
.
Аналогично можно получить, что
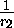 =
= 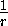 -
- 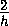 , откуда r1=r2 .
, откуда r1=r2 .
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет