Олимпиадная задача: квадратные трёхчлены и модуль на производных, 10-11 класс
Задача
Квадратные трёхчлены f(x) и g(x) таковы, что f '(x)g'(x) ≥ |f(x)| + |g(x)| при всех действительных x.
Докажите, что произведение f(x)g(x) равно квадрату некоторого трёхчлена.
Решение
Пусть u, v – абсциссы вершин парабол y = f(x) и y = g(x). Тогда f(x) = a(x – u)² + b, g(x) = c(x – v)² + d (a, c ≠ 0), и исходное неравенство переписывается в виде 4ac(x – u)(x – v) ≥ | a(x – u)² + b| + |c(x – v)² + d|. Подставляя в это неравенство x = u, получаем |b| + |c(x – v)² + d| ≤ 0, откуда b = 0 и c(u – v)² + d = 0. По аналогичным соображениям d = 0, поэтому из предыдущего равенства следует, что u = v. Так как 4ac(x – u)² ≥ 0 при всех x, то ac > 0. Поэтому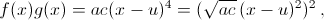 
что и требовалось.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь