Олимпиадная задача Френкина: решить систему уравнений на корни и степени (10-11 класс)
Задача
Решите систему уравнений (n > 2) 
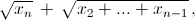 x1 – x2 = 1.
x1 – x2 = 1.
Решение
Пусть x1 + x2 + ... + xn = S. Возведя равенство 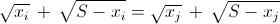 в квадрат и приведя подобные, получим
xi(S – xi) = xj(S – xj) ⇔ (xi – xj)(xi + xj – S) = 0.
Таким образом, для каждой пары неизвестных либо xi = xj, либо xi + xj = S.
в квадрат и приведя подобные, получим
xi(S – xi) = xj(S – xj) ⇔ (xi – xj)(xi + xj – S) = 0.
Таким образом, для каждой пары неизвестных либо xi = xj, либо xi + xj = S.
x1 > x2, поэтому x1 + x2 = S. Поскольку все неизвестные неотрицательны, x3 = x4 = ... = xn = 0.
x2 + x3 = x2 < S, следовательно, x2 = x3 = 0.
Ответ
(1, 0, ..., 0).
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет