Олимпиадная задача по планиметрии для 8-9 класса: отношение DK к AB
Задача
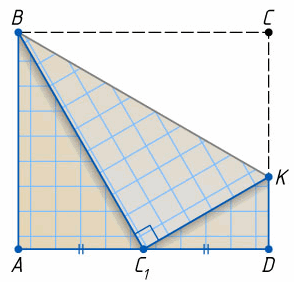
Прямоугольный лист бумаги ABCD согнули так, как показано на рисунке. Найдите отношение DK : AB, если C1 – середина AD.
Решение
AC1 = DC1 = ½ AD. Треугольники BC1K и BCK равны, значит, BC1 = BC. В прямоугольном треугольнике ABC1 катет AC1 равен половине гипотенузы BC1, значит, ∠ABC1 = 30°. Поэтому ∠AC1B = 60°, ∠DC1K = 180° – 60° – 90° = 30°.
В прямоугольном треугольнике KDC1 катет, лежащий против угла в 30° равен половине гипотенузы, то есть DK = ½ C1K = ½ CK, а так как
DK + CK = CD, то DK = ⅓ CD.
Ответ
1 : 3.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет