Олимпиадная задача по математике: цвета полусуммы чисел одной четности, 9–11 класс

  а) Рассмотрим какой-нибудь цвет, например, красный. Найдём два числа красного цвета, разность которых делится на 8 (такие найдутся, потому что число остатков при делении на 8 конечно и, взяв два красных числа с одинаковым остатком, мы получаем искомую пару). Обозначим эти числа через a и b, а цвет числа  ½ (a + b)  через Ц₁. При этом  ¼ (3a + b)  и  ¼ (a + 3b)  имеют один и тот же цвет Ц₂ (полусумма чисел красного цвета и Ц₁).

  Числа  ⅛ (7a + b),  ⅛ (5a+ 3b),  ⅛ (3a+ 5b),  ⅛ (a+ 7b),  ¼ (a+ 3b),  ⅛ (3a+ 5b) имеют один и тот же цвет Ц₃(полусумма чисел красного цвета и Ц₂). Так как числа  ½ (a + b),  ⅛ (3a+ 5b)  являются полусуммами чисел цвета Ц₃, то цвета Ц₁, Ц₂и Ц₃совпадают.   Рассмотрим цвет числа  ⅛ (9b – a)  Пусть это Ц₄. Тогда  ⅛ (a+ 7b)  иbявляются полусуммами чисел цвета Ц₄и Ц₁и поэтому имеют одинаковый цвет. Таким образом, Ц₁– это красный цвет, что и требовалось доказать.   б) Если N нечётно, то можно сделать следующую раскраску: покрасить число в цвет  j ∈ {0, ...,  N – 1},  если оно имеет остаток j от деления на N. Легко видеть, что такая раскраска удовлетворяет условию.

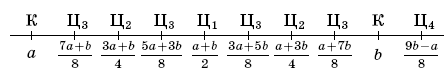
  Теперь докажем, что для любой раскраски, удовлетворяющей условию, N нечётно.

  Докажем, что для каждого цвета (например, красного) последовательность чисел, окрашенных в него, является арифметической прогрессией с нечётной разностью. Обозначим эту последовательность через  a₁ < a₂ < ... Докажем индукцией по n, что a₁, ..., a_n – арифметическая прогрессия с нечётной разностью.   База. При  n = 1  в прогрессии один член и доказывать нечего. При  n = 2  разность  a₂ – a₁  нечётна, потому что иначе число

½ (a₁ + a₂)  было бы красного цвета (см. а).

  Шаг индукции. Предположим, что  a_n+1 – a_n  чётно. Тогда число  ½ (a_n + a_n+1)  красное. Противоречие. Значит,  a_n+1 – a_n нечётно. Поэтому и по предположению индукции  a_k+1 – a_k–1  чётно. Значит, число  ½ (a_n–1 + a_n+1)  красное. Поэтому  ½ (a_n–1 + a_n+1) = a_n   Пусть d₁, ..., d_N – разности прогрессий, D – наименьшее общее кратное всех d_j,  a = max b_j,  где b_j – минимальное число цвета j. Тогда среди чисел

a + 1, ..., a + D  ровно ^D/_dj чисел цвета j (так как числа цвета j образуют прогрессию с разностью d_j). Значит,  D = Σ ^D/_dj.  Следовательно,  Σ ¹/_dj = 1.

  Приведя в этой сумме все дроби к общему знаменателю, получим в знаменателе нечётное число, а в числителе – сумму N нечётных слагаемых, равную знаменателю, и значит, нечётную. Поэтому N нечётно.

б) При чётных N.