Олимпиадная задача по тригонометрии для 9-11 классов: неравенство синусов в остроугольном треугольнике
Задача
Докажите, что если α , β и γ – углы остроугольного треугольника, то sinα + sinβ + sinγ > 2.
Решение
Первый способ ("тригонометрический").Докажем сначала вспомогательное утверждение:
Если α , β и γ – углы произвольного треугольника, то cos2α+ cos2β+ cos2γ+2 cosα cosβ cosγ=1.
Действительно, так как γ=180o-(α+β), то cos2α+ cos2β+ cos2γ+2 cosα cosβ cosγ-1 =
cos2α+ cos2β+ cos2(α+β)-2 cosα cosβ cos(α+β)-1 =
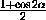 +
+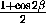 -1 + cos2(α+β)-2 cosα cosβ cos(α+β) =
-1 + cos2(α+β)-2 cosα cosβ cos(α+β) =
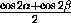 + cos2(α+β)-( cos(α+β)+ cos(α-β)) cos(α+β) =
cos(α+β) cos(α-β)+ cos2(α+β)- cos2(α+β)- cos(α-β) cos(α+β) = 0.
Так как данные углы– острые, то из доказанного утверждения следует, что cos2α+ cos2β+ cos2γ=1-2 cosα cosβ cosγ < 1, поэтому sin2α+ sin2β+ sin2γ=3-( cos2α+ cos2β+ cos2γ) > 2.
Так как для любого угла x треугольника sin x> sin2 x , то sinα+ sinβ+ sinγ> sin2α+ sin2β+ sin2γ > 2,
что и требовалось доказать.
Второй способ("геометрический").
+ cos2(α+β)-( cos(α+β)+ cos(α-β)) cos(α+β) =
cos(α+β) cos(α-β)+ cos2(α+β)- cos2(α+β)- cos(α-β) cos(α+β) = 0.
Так как данные углы– острые, то из доказанного утверждения следует, что cos2α+ cos2β+ cos2γ=1-2 cosα cosβ cosγ < 1, поэтому sin2α+ sin2β+ sin2γ=3-( cos2α+ cos2β+ cos2γ) > 2.
Так как для любого угла x треугольника sin x> sin2 x , то sinα+ sinβ+ sinγ> sin2α+ sin2β+ sin2γ > 2,
что и требовалось доказать.
Второй способ("геометрический").
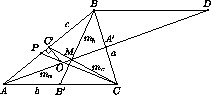
Отметим, что доказанное неравенство справедливо для любого треугольника.
Докажем теперь, что в остроугольном треугольнике ma + mb + mc 4R . Пусть М – точка пересечения медиан,
а О – центр описанной окружности остроугольного треугольника АВС (см. рис. 11.6). Так как О расположена внутри
треугольника АВС , то она принадлежит одному из трех треугольников АМВ , ВМС или СМА . Без ограничения общности
можно считать, что это треугольник АМВ , тогда АM + ВM
4R . Пусть М – точка пересечения медиан,
а О – центр описанной окружности остроугольного треугольника АВС (см. рис. 11.6). Так как О расположена внутри
треугольника АВС , то она принадлежит одному из трех треугольников АМВ , ВМС или СМА . Без ограничения общности
можно считать, что это треугольник АМВ , тогда АM + ВM  АО + ВО , то есть
АО + ВО , то есть 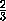 ma +
ma + 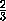 mb
mb  2R
2R
 ma + mb
ma + mb  3R .
3R .
Продолжим
отрезок СО до пересечения с АВ в точке Р . Так как угол ОС'P – прямой, то угол С'ОP – острый,
поэтому угол СOC' – тупой. Следовательно, СC1 СO , то есть mc
СO , то есть mc R .
R .
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь