Олимпиадная задача по планиметрии: расположение точек внутри треугольника ABC

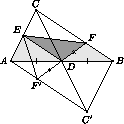
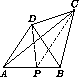
Первый способ. Рассмотрим произвольный треугольник АВС с точками E и F на сторонах АС и ВС . Пусть С' – образ точки С , а F' – образ точки F при симметрии с центром в точке D (см. рис. 11.5.1). Тогда четырехугольник ACBС' – параллелограмм, а точка F' лежит на его стороне АС' . Так как ЕАF' = ЕАB + BAF' = CАB + CBA < 180^o , то четырехугольник AEDF' – выпуклый (это следует также из того, что ЕАF – угол параллелограмма). Треугольники AF'D и BFD равны, значит, S_AEDF'=S_AED+S_AF'D= S_AED+S_BFD . Кроме того, так как D – середина отрезка FF' , то S_DEF=S_DEF' . Так как S_AEDF'>S_DEF' , то S_AED+S_BFD>S_DEF , следовательно, указанным образом расположить точки невозможно.

Второй способ. Воспользуемся вспомогательным утверждением: пусть в четырехугольнике АВСD А + В < 180^o , тогда S_BDA>S_CDA (см. рис. 11.5.2). Действительно, в силу заданного условия, прямая, проходящая через точку С и параллельная стороне AD пересекает прямую АВ в точке Р , лежащей между А и В . Тогда S_BDA>S_PDA , а треугольники РDA и CDA равновелики, так как сторона AD у них общая и высоты, проведенные из вершин Р и С равны.

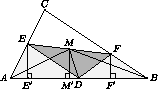
Рассмотрим теперь конфигурацию, заданную в условии задачи (см. рис. 11.5.3). Пусть М – середина отрезка EF , точки Е' , M' и F' – ортогональные проекции точек Е , M и F на прямую АВ . Тогда MM' – средняя линия трапеции EFF'E' , поэтому MM'=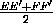 . Следовательно, S_AED+S_BFD =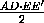+ 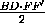= 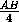(EE'+FF')=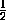AB· MM'=S_AMB .

Проведем общую медиану MD треугольников АМВ и EDF . В четырехугольнике ADME рассмотрим сумму углов ЕАD и MDA , а в четырехугольнике BDMF – сумму углов FBD и MDB . Хотя бы одна из этих сумм меньше, чем180^o . Действительно, предположим противное, тогда( EAD + MDA) + ( FBD + MDB) = ( EAB + FBA) + ( MDA + MDB) = CAB + CBA + 180^o 360^o , что невозможно, так как сумма двух углов треугольника меньше, чем180^o .

Без ограничения общности можно считать, что EAD + MDA < 180^o . Тогда в четырехугольнике ADME S_ADM>S_EDM . Так как медиана треугольника делит его площадь пополам, то S_AMB>S_EDF , то есть указанным образом расположить точки нельзя.

так расположить точки нельзя.