Олимпиадная задача по математике: экстремумы непрерывной функции, 10–11 класс
Задача
Непрерывная функция f(x)такова, что для всех действительных x выполняется неравенство: f(x2)-(f(x))2
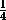 . Верно ли, что функция f(x)обязательно имеет точки экстремума?
. Верно ли, что функция f(x)обязательно имеет точки экстремума?
Решение
При x = 0получим, что f(0)-(f(0))2
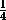
 (f(0))2-f(0)+
(f(0))2-f(0)+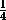
 0
0 (f(0)-
(f(0)-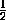 )2
)2 0
0
 f(0)=
f(0)=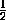 . Аналогично, при x = 1: f(1)-(f(1))2
. Аналогично, при x = 1: f(1)-(f(1))2
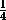
 f(1)=
f(1)=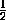 .
.
Так как непрерывная функция принимает одинаковые значения на концах[0; 1], то внутри этого отрезка есть хотя бы одна точка максимума или точка минимума.
Отметим, что если 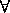 x
x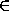 [0; 1] f(x) =
[0; 1] f(x) =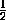 , то любая точка этого отрезка является точкой экстремума.
, то любая точка этого отрезка является точкой экстремума.
Ответ
да, верно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет