Олимпиадная задача по стереометрии: угол при вершине осевого сечения конуса
Задача
Найдите угол при вершине осевого сечения прямого кругового конуса, если известно, что существуют три образующие боковой поверхности конуса, попарно перпендикулярные друг другу.
Решение
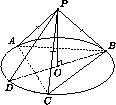
Из условия задачи следует, что в данный конус может быть вписана треугольная пирамида РАВС , у которой равны боковые ребра РА , РВ и РС , и все плоские углы при вершине Р – прямые (см. рис. 11.3). Следовательно, эта пирамида– правильная и ее высотой является отрезок РО , где О – центр основания конуса. Тогда искомый угол BPD вдвое больше угла ВРО .
Пусть PB = b , тогда BC = b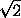
; OB=
=
.
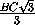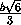Тогда sin
BPO=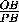
=
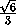; BPD = 2 arcsin .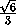
Если вычислять искомый угол по теореме косинусов из треугольника BPD, то ответ можно получить в другом виде BPD = arccos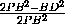
= arccos(-
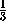)=π - arccos .
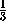В любом случае искомый угол– тупой.
Ответ
2 arcsin .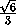
Чтобы оставлять комментарии, войдите или зарегистрируйтесь