Олимпиадная задача по планиметрии: Высоты в остроугольном треугольнике, 8-9 класс
Задача
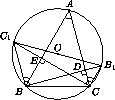
Высоты остроугольного треугольника ABC, проведенные из точек B и C, продолжили до пересечения с описанной окружностью в точках B1 и C1. Оказалось, что отрезок B1C1 проходит через центр описанной окружности. Найдите угол BAC.
Решение
Так как B1C1 – диаметр окружности, то ∠B1BC1 = ∠B1CC1 = 90°, следовательно, BC1 || AC и CB1 || AB (см. рис.). Так как BC1 || AC, то
∠C1BA = ∠A = α. Аналогично ∠B1CA = ∠A = α. Градусная мера дуги B1C1 равна 180°, поэтому сумма вписанных углов C1BA и B1CA равна 90°, то есть ∠A = 45°.
Ответ
45°.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет