Олимпиадная задача Канель-Белова: делимость многочленов и простые числа (9-11 классы)

  Заметим, что 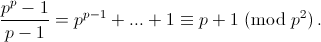    Значит, у этого числа есть простой множитель  q ≠ 1 (mod p²).  При этом   p^p – 1  делится на q.

  Предположим, что  n^p ≡ p (mod q).  Тогда  n^p2 ≡ p^p ≡ 1 (mod q).  С другой стороны, n, очевидно, не кратно q, и по малой теореме Ферма (см. задачу 160736)

n^q–1 ≡ 1 (mod q).  Так как  q – 1  не делится на p², наибольший общий делитель чисел p² и  q – 1  равен p или 1. В любом случае  p ≡ n^p ≡ 1 (mod q).

  Отсюда следует, что  0 ≡ p^p–1 + ... + p + 1 ≡ p (mod q).  Противоречие.

Ответ задачи отсутствует