Олимпиадная задача по теории множеств: 101-элементное подмножество и непресекающиеся сдвиги

Рассмотрим множество  D = {x – y|  x, y ∈ A}.  В нём не более чем  10101 = 101·100 + 1  элемент. Ясно, что условие  A_i ∩ A_j = ∅  равносильно тому, что  t_i – t_j ∉ D.  Будем выбирать t_i по одному. t₁ выберем произвольно. Предположим, что  t₁, ..., t_m,  m ≤ 99,  уже выбраны. Новое t_m+1 можно выбрать произвольно из дополнения к 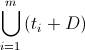  .   Это дополнение не пусто, ибо число элементов в множестве  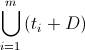   не превосходит

|D|m ≤ 10101m < 10⁶.

Ответ задачи отсутствует