Олимпиадная задача по планиметрии и комбинаторной геометрии для 9-10 классов: невыпуклый шестиугольник
Задача
В невыпуклом шестиугольнике каждый угол равен либо 90, либо 270 градусов. Верно ли, что при некоторых длинах сторон его можно разрезать на два подобных ему и неравных между собой шестиугольника?
Решение
Пусть t – корень уравнения t4+t2=1. Возьмем
шестиугольник ABCDEF , в котором AB:BC=BC:CD=CD:AF=AF:FE=FE:ED=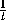 , и разрежем его, как
на рис.9.4. Тогда получившиеся шестиугольники подобны ABCDEF с
коэффициентами t и t2 .
, и разрежем его, как
на рис.9.4. Тогда получившиеся шестиугольники подобны ABCDEF с
коэффициентами t и t2 .
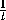
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет