Олимпиадная задача по планиметрии: окружность, хорды и фиксированная окружность, 9–11 класс

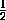Пусть O – центр данной окружности, O' – центр окружности, проходящей через середины сторон ABC , P – центр тяжести ABC . Поскольку вершины треугольника ABC переходят в середины его сторон при гомотетии с центром P и коэффициентом - , P лежит на отрезке OO' и делит его в отношении2:1. Кроме того, так как множество середин хорд, проходящих через M ,– это окружность с диаметром OM , множество центров тяжести треугольников ABC – тоже окружность, получающаяся из нее гомотетией с центром A и коэффициентом 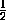. Значит, множество точек O' – тоже окружность (рис.9.2).

Поскольку радиусы всех окружностей, проходящих через середины сторон ABC , равны половине радиуса данной окружности, все эти окружности касаются двух окружностей, концентричных с окружностью, на которой лежат точки O' (если точка M совпадает с O , одна из этих окружностей вырождается в точку).

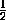
Ответ задачи отсутствует