Олимпиадная задача по планиметрии: Окружности и касательные (7–9 классы)
Задача
Дана окружность радиуса R. Две другие окружности, сумма радиусов которых также равна R, касаются её изнутри.
Докажите, что прямая, соединяющая точки касания, проходит через одну из общих точек этих окружностей.
Решение
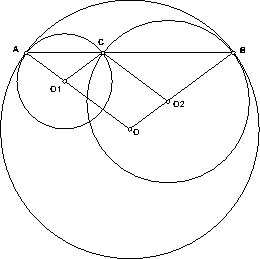
ПустьO– центр внешней окружности,O1,O2– центры внутренних,A, B– точки касания. Проведём черезO1прямую, параллельнуюOB, а черезO2– прямую, параллельнуюOA. Поскольку O1O = O2B и O2O = O1A, то теореме Фалеса эти прямые пересекутся в точкеC, лежащей на отрезкеAB. При этом O1C = O1A и O2C = O2B, так что точкаCпринадлежит обеим внутренним окружностям (см. рис.).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет