Математическая задача по олимпиадной геометрии 7-9 класс: многоугольник, стороны и диагонали

Олимпиадная задача по планиметрии: Многоугольник со сторонами и диагоналями — 7-9 класс

Задача

Существует ли выпуклый многоугольник, у которого каждая сторона равна какой-нибудь диагонали, а каждая диагональ– какой-нибудь стороне?

Решение

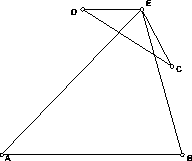
Ответ: нет. Предположим противное, и пусть AB – наибольшая сторона многоугольника, CD – наименьшая диагональ ( AB и CD могут иметь один общий конец), E – вершина, лежащая от CD по другую сторону, чем A и B (рис.8.5). Тогда, так как AE AB и BE AB , AEB 60^o . С другой стороны, так как CE CD и DE CD , CED 60^o . Но CED> AEB – противоречие.