Олимпиадная задача по планиметрии для 7-9 классов: параллелограмм и окружности (Протасов В. Ю.)
Задача
Дан параллелограмм ABCD. Две окружности с центрами в вершинах A и C проходят через D. Прямая l проходит через D и вторично пересекает окружности в точках X, Y. Докажите, что BX = BY.
Решение
Рассмотрим случай, изображенный на рис. Имеем AX = AD = BC и CY = CD = AB. Кроме того,
∠BCY = ∠C – ∠DCY = ∠C – (π – 2∠CDY) = 2∠CDY – ∠D = ∠CDY – ∠ADX, ∠BAX = ∠DAX – A = π – 2∠ADX – ∠A = ∠D – 2∠ADX = ∠CDY – ∠ADX. Значит, треугольники ABX и CYB равны, откуда и следует искомое равенство.
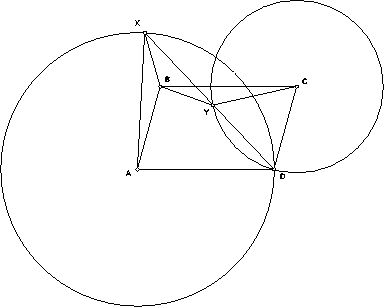
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет