Олимпиадная задача по планиметрии и комбинаторной геометрии для 7-9 классов: разрезание n-угольника
Задача
При каком наименьшем n существует n -угольник, который можно разрезать на треугольник, четырехугольник, ..., 2006-угольник?
Решение
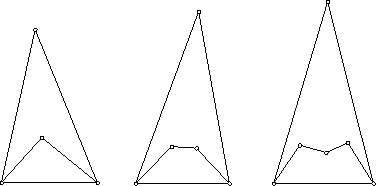
При n=3. Из рисунка видно, что при любом n 3треугольник можно разрезать на n -угольник и(n+1)-угольник. Следовательно, можно лучами, выходящими из одной
вершины, разрезать треугольник на 1002 треугольника, а затем
первый из них разрезать на треугольник и четырехугольник, второй
на пятиугольник и шестиугольник, последний – на
2005-угольник и 2006-угольник.
3треугольник можно разрезать на n -угольник и(n+1)-угольник. Следовательно, можно лучами, выходящими из одной
вершины, разрезать треугольник на 1002 треугольника, а затем
первый из них разрезать на треугольник и четырехугольник, второй
на пятиугольник и шестиугольник, последний – на
2005-угольник и 2006-угольник.
Ответ
При n=3.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет