Олимпиадная задача по планиметрии: вписать треугольник наибольшего периметра

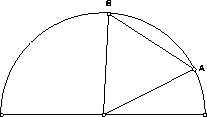
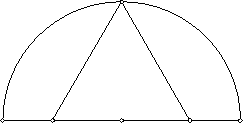
  Очевидно, вписать треугольник в полукруг можно двумя способами: либо две вершины треугольника лежат на дуге, а третья на диаметре полукруга, либо, наоборот, две вершины на диаметре, а третья на дуге. Рассмотрим первый случай. Пусть вершины A, B лежат на дуге. Тогда серединный перпендикуляр к AB проходит через центр полукруга. Следовательно, третья вершина совпадает с центром и сторона треугольника равна радиусу полукруга (рис. слева).

  Во втором случае высота треугольника не превосходит радиуса полукруга, причём в случае, изображённом на рис. справа, равенство достигается. Следовательно, именно этот треугольник и будет искомым.

Ответ задачи отсутствует