Олимпиадная задача по планиметрии и комбинаторной геометрии для 9–10 класса: пятизвенная ломаная

Пусть O – точка пересечения прямых. Возьмём на прямой l₁ точку A₁ и найдём на l₃ такую точку A₂, что середина B отрезка A₁A₂ лежит на прямой l₂ (см. рис.). Применяя теорему синусов к треугольникам OA₁B и OA₂B, получаем, что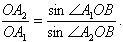  

Аналогично по точкеA₂построим на прямойl₅такую точкуA₃, что серединаA₂A₃лежит наl₄и т.д. Перемножив полученные соотношения, получим, чтоA₆совпадает сA₁.

Ответ задачи отсутствует