Олимпиадная задача по планиметрии о треугольнике и центр вписанной окружности, 8–9 класс

ПустьÐA = α,ÐB = β,ÐC = γ. ПосколькуÐPBA+ÐPCA+ÐPBC+ÐPCB= β + γ, условие задачи эквивалентноÐPBC+ÐPCB= (β + γ)/2, т.е.ÐBPC= π/2 + α/2.

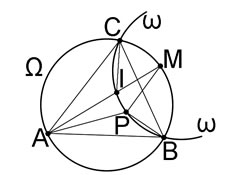
С другой стороны,ÐPIC= π - (β + γ)/2 = π/2 + α/2. Следовательно,ÐBPC=ÐPIC, и т.к. точкиPиIлежат по одну сторону отBC, точкиB,C,IиPлежат на одной окружности. Иными словами,Pлежит на ω - описанной окружности ΔBCI.

Пусть Ω - описанная окружность ΔABC. Легко проверить, что центр окружности ω совпадает с серединой дугиBCи лежит на Ω, а значит - и на биссектрисе углаCAB. Из неравенства треугольника (для ΔAPM) следует

|AP| + |PM| ≥ |AM| = |AI| + |IM| = |AI| + |PM|

Поэтому |AP| ≥ |AI|. Равенство достигается тогда и только тогда, когдаPпринадлежит [AI], что означаетP = I.

Ответ задачи отсутствует