Олимпиадная задача по планиметрии для 9–10 классов: равнобедренные трапеции
Задача
На основании AD и боковой стороне AB равнобедренной трапеции ABCD взяты точки E, F соответственно так, что CDEF – также равнобедренная трапеция. Докажите, что AE·ED = AF·FB.
Решение
Решение 1:Из условия следует, что ∠DCF = ∠CDA = ∠DAB = ∠FEA (см. рис.). Следовательно, ∠ BCF = ∠AFE и
BF : ED = BF : FC = sin∠BCF : sin∠CFB = sin∠AFE : sin∠FNA = AE : AF, что и требовалось.
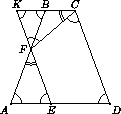
Решение 2:Пусть прямая EF пересекает BC в точке K. Тогда ∠FKC = ∠FEA = ∠CDA = ∠BAD = ∠KFC, поэтому равнобедренные треугольники CFK и FAE подобны, и CF : AF = FK : AE = FB : AE. Отсюда DE·AE = CF·AE = FB·AF.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет