Олимпиадная задача по планиметрии: три попарно похожих треугольника. 8-9 класс
Задача
Назовём два неравных треугольника похожими, если можно обозначить их ABC и A'B'C' так, чтобы выполнялись равенства AB = A'B', AC = A'C' и
∠B = ∠B'. Существуют ли три попарно похожих треугольника?
Решение
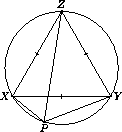
Например, пусть XYZ – правильный треугольник, P – точка на дуге XY описанной около него окружности, отличная от середины дуги (см. рис.). Тогда треугольники XPY, YPZ, ZPX попарно не равны. При этом в треугольниках XPZ и YPZ сторона PZ общая, XZ = YZ и ∠XPZ = ∠YPZ = 60°. В треугольниках XPZ и XPY сторона XP общая, XZ = XY и ∠PZX = ∠PYX. Аналогично находятся равные элементы в треугольниках PXY и PYZ.
Ответ
Существуют.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет