Олимпиадная задача по планиметрии: восстановление треугольника ABC по точкам

Решение 1:   При симметрии относительно биссектрисы угла B точка A переходит в лежащую на этой же прямой точку A', причём  BA' = BA.  Для любой лежащей на биссектрисе точки L имеем  LA = LA',  а поскольку  BA > BC,  точки A' и L лежат по разные стороны от прямой AC (см. рис.).

  Таким образом, получаем следующее построение.   Проведём черезCпрямуюl, перпендикулярнуюAC. Проведём окружность с центромLи радиусомLAи найдём точкуA'ее пересечения сl, лежащую сLпо разные стороны отAC. Проведём серединный перпендикуляр к отрезкуAA'и найдём точкуBего пересечения сl.

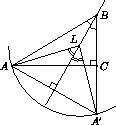
Решение 2:   Проведём прямую BC – перпендикуляр к AC. Построим окружность c центром в точке L, касающуюся BC. Так как BL – биссектриса, то эта окружность касается также и AB. Тогда точка B – это точка пересечения BC и луча из точки A, касающегося нашей окружности. При этом точка пересечения AL и BC лежит на отрезке BC (см. рис.).

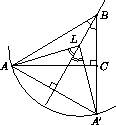
Решение 3:   Строим прямую BC. Пусть K – точка пересечения AL и BC. Тогда BL – биссектриса треугольника ABK, и точка B лежит на окружности Аполлония для отрезка AK и точки L внутри него. При этом опять надо из двух точек пересечения брать дальнюю от C.

Ответ задачи отсутствует