Олимпиадная задача по стереометрии: каркас многогранника после параллельных переносов

Первое решение.Нет. Рассмотрим, например, правильный икосаэдр. Пять его граней, имеющие общую вершину, являются боковыми гранями правильной пятиугольной пирамиды. Центры этих граней образуют правильный пятиугольник, стороны которого параллельны сторонам основания пирамиды. Поэтому ребра икосаэдра параллельны ребрам додекаэдра, образованного центрами его граней. Следовательно, параллельно перенеся ребра икосаэдра, можно получить додекаэдр. Второе решение. Рассмотрим призму ABCA'B'C' с разносторонним треугольником ABC в основании. Пусть B₁ – середина BB' , а точки A₁ и C₁ расположены на ребрах AA' и CC' так, что AA₁=C'C₁ (рис.10.5).

Тогда в многогранниках ABCA₁B₁C₁ и A'B'C'A₁B₁C₁ ребра удовлетворяют условию. Легко подобрать параметры так, чтобы все ребра в каждом из них были различными, а двугранный угол при AB – непрямым. Тогда эти многогранники не могут быть равными, так как двугранные углы при одинаковых ребрах AB и A'B' дополнительны и потому различны.

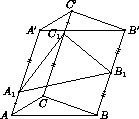
Ответ задачи отсутствует