Олимпиадная задача по планиметрии: симметрия прямых в четырехугольнике ABCD

Первое решение.Покажем, что произведения расстояний от O до противоположных сторон четырехугольника равны. Действительно, если X , Y – проекции D' на BC и AB , а X' , Y' – основания высот треугольника ABC , опущенных на эти же стороны, то отношение расстояний от O до AD и CD равно

= === ,

т.е. отношению расстояний от O до AB и BC . Покажем, что по трем вершинам четырехугольника, обладающего этим свойством, четвертая определяется однозначно, т.е. оно равносильно как условию задачи, так и ее заключению.

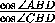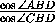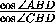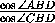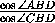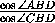
Итак, пусть ABCD – вписанный четырехугольник, в котором произведения расстояний от центра описанной окружности до противоположных сторон равны. Рассмотрим четырехугольник AB₁CD₁ , где B₁ , D₁ – точки, диаметрально противоположные B , D . Очевидно, что, например, AB₁ равно удвоенному расстоянию от центра окружности до AB , т.е. наше свойство равносильно тому, что четырехугольник AB₁CD₁ – гармонический. Но в гармоническом четырехугольнике три вершины однозначно определяют четвертую. Второе решение. Отметим на нашей окружности σ точки C'' и D'' такие, что BD и BD'' симметричны относительно биссектрисы угла B , а AC и AC'' симметричны относительно биссектрисы угла A . 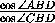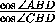Тогда имеем AD''=DC=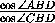 , то есть C'' и D'' симметричны относительно серединного перпендикуляра d к отрезку AB . Заметим, что точки B , D' и D'' лежат на одной прямой.

Выясним, как строятся точки C' и D' . Пусть отрезок A'B' симметричен отрезку AB относительно O , а – прямая, параллельная AB и проходящая через точку O – центр σ . Тогда вторая точка пересечения высоты CH_C треугольника ABC с σ получается из C симметрией относительно , а ортоцентр H_C из этой точки – симметрией относительно AB ; наконец, D' получается из H_C симметрией относительно O . Композиция этих трех преобразований – симметрия относительно середины K отрезка A'B' (см. рис.10.4.2). Итак, точки C' и D' лежат на окружности σ' , симметричной σ относительно K .

Суммируем полученные результаты. Нам нужно доказать, что точки A , C' , C'' лежат на одной прямой, то есть – что прямые BD' и AC' симметричны относительно d . Покажем для этого, что точка C' при отражении относительно d попадает на прямую BD' , а точнее – во вторую точкой пересечения BD' и σ' (обозначим эту точку через D₀' ). Это эквивалентно тому, что D и D₀' симметричны относительно A'B' .

Итак, пусть D₀ – точка, симметричная D₀' относительно A'B' . Тогда

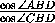
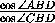AD''=2 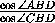ABD''=2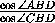(B'A',D'D'')=+=+,

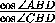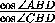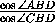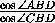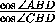последнее равенство – в силу симметрий. Итак, AD''=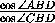D₀C , что и означает D=D₀ .

Ответ задачи отсутствует