Олимпиадная задача по планиметрии для 8–10 классов от Протасова В. Ю.: доказательство положения точек в остроугольном треугольнике
Задача
Точки A', B', C' – основания высот остроугольного треугольника ABC. Окружность с центром B и радиусом BB' пересекает прямую A'C' в точках K и L (точки K и A лежат по одну сторону от BB'). Докажите, что точка пересечения прямых AK и CL лежит на прямой BO, где O – центр описанной окружности треугольника ABC.
Решение
Решение 1:Так как ортоцентр треугольника ABC является центром вписанной окружности треугольника A'B'C' (см. задачу 152866), точка, симметричная B' относительно AB, лежит на прямой A'C', то есть совпадает с K. Аналогично, B' и L симметричны относительно BC. Отсюда следует, что ∠AKC' = ∠AB'C' = ∠CB'A' = ∠CL'A', то есть точка пересечения AK и CL лежит на серединном перпендикуляре к отрезку KL. Так как BK = BB' = BL, этот серединный перпендикуляр совпадает с биссектрисой угла KBL, которая в силу равенства ∠OBA = 90° – ∠C = ∠B'BC проходит через O (рис. слева).
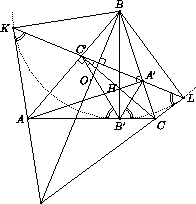
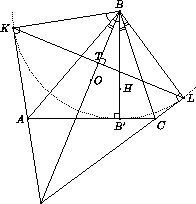
Решение 2:Пусть BT – высота треугольника BA'C'. Из подобия BA'C' и BCA имеем BT : BK = BT : BB' = BA' : BC = cos∠ABC, поэтому ∠KBT = ∠ABC = ∠LBT. Значит,
∠KBA = ∠KBT – ∠ABT = ∠ABC – ∠CBB' = ∠ABB'. Следовательно, точки K и B' симметричны относительно AB, поэтому AK (и аналогично CL) – касательные к нашей окружности в точках K и L. Они пересекаются на биссектрисе угла KBL, то есть на прямой BT (рис. справа). Но, как известно, точка O тоже лежит на прямой BT (см. задачу 156510 б).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь