Олимпиадная задача по планиметрии: восстановление треугольника по точкам пересечения

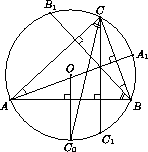
Пусть биссектриса угла C пересекает описанную окружность треугольника ABC в точке C₀ , а высоты, проведенные из вершин A , B – в точках A₁ , B₁ . Так как A₁AC= B₁BC=90^o- C , точка C является серединой дуги A₁B₁ , не содержащей C₀ . Далее, прямая OC₀ является серединным перпендикуляром к AB , и значит, параллельна высоте, проведенной из C . Проведя эту высоту, найдем вторую точку C₁ ее пересечения с окружностью и затем найдем точки A , B , как середины дуг B₁C₁ и A₁C₁ (рис.10.1).

Ответ задачи отсутствует