Олимпиадная задача по стереометрии: параллелепипед вписан в сферу, класс 10–11
Задача
В сферу радиуса 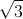 вписан параллелепипед, объём которого
равен 8. Найдите площадь полной поверхности параллелепипеда.
вписан параллелепипед, объём которого
равен 8. Найдите площадь полной поверхности параллелепипеда.
Решение
Поскольку около параллелепипеда описана сфера, этот параллелепипед – прямоугольный. Обозначим его рёбра, исходящие из одной вершины, через a, b и c. Диагонали параллелепипеда равны диаметру описанной сферы, а объём равен abc. Из условия задачи следует, что a² + b² + c² = 12, abc = 8.
Согласно неравенству Коши 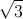 Поскольку равенство достигается, только когда a² = b² = c², то
Поскольку равенство достигается, только когда a² = b² = c², то
a = b = c = 2. Следовательно, площадь поверхности равна 6a² = 24.
Ответ
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет