Олимпиадная задача по математике: доказательство равенства чисел — 7-9 класс

  Пусть  ^a/_c = ^b/_d = ^ab+1/_cd+1 = ¹/_r  (то есть  c = ra,  b = rd).  Тогда 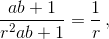    или  rab + r = r²ab + 1.  Отсюда  (rab – 1)(r – 1) = 0,  то есть либо  r = 1  (и тогда  a = c  и  b = d),  либо  rab = 1.

  Но  rab = cb = 1,  то есть  c = b = 1;  аналогично  a = d = 1.  В обоих случаях  a = c  и  b = d.

Ответ задачи отсутствует