Олимпиадная задача по алгебраическим неравенствам и функциям для 9–11 класса
Задача
Функции f(x) – x и f(x²) – x6 определены при всех положительных x и возрастают.
Докажите, что функция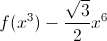 
также возрастает при всех положительных x.
Решение
Далее все функции рассматриваются только на положительной полуоси. Заметим, что возрастание функции g(xn) эквивалентно возрастанию функции g(x), а возрастание функции вида f(x) – g(x) эквивалентно условию f(x) – f(y) > g(x) – g(y) при x > y.
Итак, нам нужно доказать, что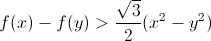 
при x > y.
Заметим, что 4(x² + xy + y²) = 3(x + y)² + (x – y)² ≥ 3(x + y)². Следовательно,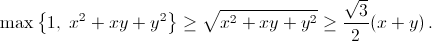 
Умножив на x – y, получаем, что 
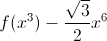при x > y. В силу возрастания указанных в условии функций f(x) – f(y) > max {x – y, x³ – y³}, и нужное неравенство доказано.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь