Олимпиадная задача по комбинаторной геометрии: раскраска доски 10×10 цветами
Задача
В какое наибольшее число цветов можно раскрасить все клетки доски размера 10×10 так, чтобы в каждой строке и в каждом столбце находились клетки не более чем пяти различных цветов?
Решение
Пример раскраски в 41 цвет показан на рисунке (неотмеченные клетки окрашены в 41-й цвет).
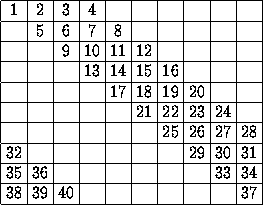
Ответ
В 41 цвет.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет