Докажите количество корней суммы парабол — олимпиадная задача по многочленам (9-11 класс)
Задача
На оси Ox произвольно расположены различные точки X1, ..., Xn, n ≥ 3. Построены все параболы, задаваемые приведёнными квадратными трёхчленами и пересекающие ось Ox в данных точках (и не пересекающие ееё в других точках). Пусть y = f1(x), ..., y = fm(x) – соответствующие параболы. Докажите, что парабола y = f1(x) + ... + fm(x) пересекает ось Ox в двух точках.
Решение
Решение 1: По условию f1(x) = (x – x1)(x – x2), f2(x) = (x – x1)(x – x3), ..., fn–1(x) = (x – x1)(x – xn), fn(x) = (x - x2)(x – x3), ..., fm(x) = (x – xn–1)(x – xn), где xi – координата точки Xi. Поэтому f1(x) + ... + fm(x) = (½ n(n – 1)x² – (n – 1)(x1 + x2 + ... + xn)x + (x1x2 + x1x3 + ... + xn–1xn)). Найдем дискриминант этого трёхчлена:
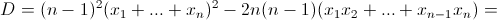
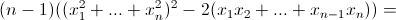
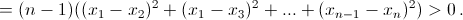
Решение 2: Прибавив к удвоенной сумме 2S = 2(f1(x) + ... + fm(x)) слагаемые y1 = (x – x1)², ..., yn = (x – xn)², получим 2S1 = ((x – x1) + (x – x2) + ... + (x – xn))² = (nx – (x1 + ... + xn))².
Видно, что S1 обращается в ноль в точке x0 = 1/n (x1 + ... + xn). Но S < S1, так как yi ≥ 0 и не более одного числа из yi может равняться нулю. Значит, S(x0) < 0, что и доказывает утверждение задачи.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь