Олимпиадная задача по теории чисел: максимальная длина арифметической прогрессии с условием простоты
Задача
Какова наибольшая длина арифметической прогрессии из натуральных чисел a1, a2, ..., an с разностью 2, обладающей свойством: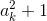 
– простое при всех k = 1, 2, ..., n?
Решение
Если a = 5m ± 2, то a² + 1 делится на 5. Это число будет простым только при a = 2. Среди чисел b, b + 2, b + 4, ... не более двух подряд идущих чисел, не имеющих вид 5m ± 2. Значит, если в прогрессии не содержится число 2, то n ≤ 2. Если a1 = 2, то n ≤ 3, так как a4 = 8 = 5·2 – 2. Числа a1 = 2,
a2 = 4, a3 = 6 дают искомую тройку: 5, 17, 37 – простые числа.
Ответ
n = 3.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет