Олимпиадная задача по комбинаторной геометрии: квадратная раскраска клетчатой плоскости для 9–11 класса

  Назовём одну из строк, в которой встречаются все цвета, выделенной. Назовём множество клеток, отстоящих друг от друга по горизонтали и вертикали на кратное n число клеток, полным.   Лемма. В полном множестве либо каждая строка, либо каждый столбец одноцветны.

  Доказательство. Предположим, что в какой-то строке нашего множества нашлись две клетки разного цвета; тогда найдутся и две клетки разного цвета на расстоянии n. Пусть это клетки a и b, а клетки полного множества над ними – x и y (см. рис.).

  Из сравнения цветов в квадратах, составленных из клеток множеств  a ∪ S₁ ∪ D  и  x ∪ S₂ ∪ D,  видно, что наборы цветов в множествах  a ∪ S₁  и  x ∪ S₂  одинаковы; аналогично одинаковы наборы цветов в  S₂ ∪ y  и  S₁ ∪ b.  Так как в множестве S₁ нет клеток цвета b, то и в множестве  x ∪ S₂  нет такого цвета; однако в  S₂ ∪ y  он есть, поэтому цвета y и b совпадают. Аналогично совпадают цвета x и a.

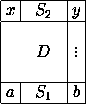
  Повторяя эти рассуждения, получаем, что столбец нашего множества, содержащий a, окрашен одинаково, и то же со столбцом b.

  Если найдутся две клетки на расстоянии n в каком-то столбце, покрашенные по-разному, то аналогично докажем, что строки множества, их содержащие, будут одноцветными. Но они пересекаются со столбцом цвета b, поэтому их цвета совпадают. Противоречие.   Назовём полное множество вертикальным, если любой его столбец одноцветен, и горизонтальным в противном случае. Докажем, что все горизонтальные полные множества пересекаются с выделенной строкой.

  Пусть это не так. Рассмотрим строку нашего множества, ближайшую к выделенной; пусть она имеет цвет a. Тогда каждую клетку выделенной строки можно заключить в квадрат n×n вместе с какой-то клеткой цвета a из нашего горизонтального множества; поэтому в выделенной строке нет цвета a. Противоречие.

  Пусть каждый столбец пересекается с горизонтальным полным множеством. Тогда выделенная строка пересекается с n горизонтальными множествами, строки которых одноцветны; поэтому в выделенной строке только n цветов. Противоречие.

  Следовательно, есть столбец, для которого все полные множества, его содержащие, вертикальны. Его раскраска периодична с периодом n, то есть в этом столбце ровно n цветов.

Ответ задачи отсутствует