Задача по олимпиадной математике Храмцова Д.: индукция, неравенства, 9

Олимпиадная задача по математике — Индукция и неравенства, Храмцов Д., 9–11 класс

Задача

Набор чисел a₀, a₁, ..., a_n удовлетворяет условиям: a₀ = 0, a_k+1 ≥ a_k + 1 при k = 0, 1, ..., n – 1. Докажите неравенство

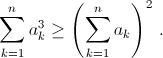
Решение

Будем доказывать утверждение по индукции. База (n = 1) очевидна.

Шаг индукции. Согласно предположению индукции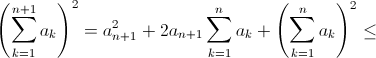

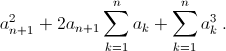
Таким образом, достаточно проверить, что 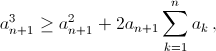или что 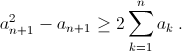Для доказательства последнего утверждения заметим, что 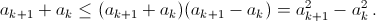Суммируя полученные неравенства поkот 0 доn, придём к неравенству 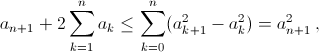что и требовалось.