Назад

Олимпиадная задача «Пирамида и сфера» по стереометрии для 10–11 классов

Задача 210086 • Сложность: 3 • 10-11 класс
Задача

Высота четырехугольной пирамиды SABCD проходит через точку пересечения диагоналей ее основания ABCD . Из вершин основания опущены перпендикуляры AA1, BB1, CC1, DD1на прямые SC , SD , SA и SB соответственно. Оказалось, что точки S , A1, B1, C1, D1различны и лежат на одной сфере. Докажите, что прямые AA1, BB1, CC1, DD1проходят через одну точку.

Авторы:
Агаханов Н. Х.
Разделы:
Планиметрия Стереометрия
Источники:
Олимпиады и турниры Всероссийская олимпиада по математике 2001-2002 Региональный этап
Количество версий:
4
Решение
Пусть SO – высота пирамиды, тогда прямые, содержащие высоты SO , AA1и CC1треугольника ASC , проходят через одну точку H1(На рисунке Δ ASC – остроугольный. Решение не изменится, если он – тупоугольный. Заметим, что прямоугольным он быть не может). Сечение данной в условиях задачи сферы σ плоскостью ASC – окружность, проходящая через точки S , A1и C1, т.е. окружность с диаметром SH1, так как углы H1A1S и H1C1S – прямые. Значит, точка H1прямой SO лежит на σ . 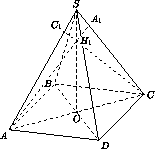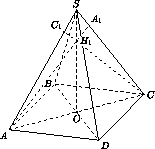Аналогично, H2σ , где H2– точка пересечения прямых SO , BB1и DD1. Из того, что H1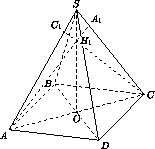 S и H2 S , следует, что H1=H2.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет