Олимпиадная задача по планиметрии: разрезание треугольника на равнобедренный

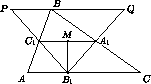
Пусть AC – большая сторона треугольника ABC, A₁C₁ – средняя линия, параллельная AC, а M – середина A₁C₁. Так как углы A и C – острые, то M проектируется внутрь отрезка AC, пусть B₁ – эта проекция (см. рис.). Проведём два разреза B₁C₁ и B₁A₁. Так как B₁M – медиана и высота треугольника A₁B₁C₁, то  C₁B₁ = A₁B₁. Пусть точка Q симметрична B₁ относительно A₁, точка P симметрична B₁ относительно C₁. Тогда треугольники BQA₁ и CB₁A₁ равны, треугольники AC₁B₁ и BC₁P также равны. Равные отрезки B₁C₁ и B₁A₁ – половины сторон треугольника PB₁Q, значит, он равнобедренный.

Ответ задачи отсутствует